Déplacer une charge⚓
Charge suspendue tractée par un câble
Question⚓
On étudie la situation ci-contre où une charge est suspendue par un câble exerçant la force \(\vec T\) verticale tout en étant tracté de A en B par un autre câble exerçant la force \({\vec F}_\text{Traction}\). Ces deux forces sont constantes au cours du mouvement.
On donne :
\(T=1500\ \mathrm N\) ;
\(F_\text{Traction}=450\ \mathrm N\) ;
\(AB=15{,}0\ \mathrm m\) ;
\(\alpha = 25°\).
Donner les expressions littérales des travaux de chacune des forces sur le déplacement de A en B.
Effectuez les applications numériques pour chacune des forces.
Que peut-on dire du travail de la force \(\vec T\) ? Était-ce prévisible ? En tirer une généralisation.
Quelles sont les forces motrices ou résistantes dans ce cas de figure ?

Solution⚓
Les deux forces étant constante au cours du déplacement, on peut écrire :
\(W_{AB}\left(\vec T \right)=\vec T \cdot \overrightarrow{AB}\) ;
\(W_{AB}\left({\vec F}_\text{Traction} \right)={\vec F}_\text{Traction} \cdot \overrightarrow{AB}=F_\text{Traction} \cdot AB \cdot \cos \alpha\).
Applications numériques :
\(W_{AB}\left(\vec T \right)=\vec T \cdot \overrightarrow{AB}=0\), car \(\vec T \perp \overrightarrow {AB}\) ;
\(W_{AB}\left({\vec F}_\text{Traction} \right)=450 \times 15{,}0 \times \cos 25 \simeq 612\ \mathrm J\).
Le travail de la force \(\vec T\) est nul. D'après l'expression mathématique du travail d'une force, on peut conclure que le travail de toute force orthogonale au déplacement est nul.
\(W_{AB}\left({\vec F}_\text{Traction} \right)>0\), donc il s'agit d'un travail moteur.
La force \(\vec T\) quant à elle ne travaille pas.
Travail du poids⚓
Base jump depuis l'Aiguille du Midi
Question⚓
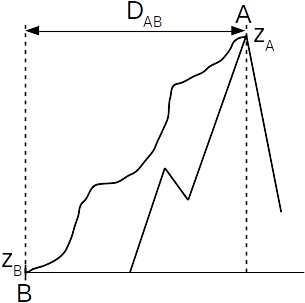
On étudie un saut en base jump depuis la gare supérieure de l'Aiguille du midi (A) située à l'altitude \(z_A=3777\ \mathrm m\) jusqu'à la vallée de Chamonix (B) à l'altitude \(z_B=1035\ \mathrm m\). La distance séparant les deux points A et B à vol d'oiseau est \(D_{AB}=1270\ \mathrm m\).
La masse du sauteur et de son équipement est \(m_\text{s}=93\ \mathrm {kg}\).
Donner l'expression littérale du travail du poids du sauteur muni de son équipement lors de ce saut et effectuer l'application numérique.
S'agit-il d'un travail moteur ou résistant ?
Solution⚓
On a montré dans le cours que le travail du poids lors d'un mouvement ne dépend que des altitudes des points de départ et d'arrivée. La distance DAB est inutile ici.
Le travail du poids entre les points A et B s'exprime donc par :
\(W_{AB}\left(\vec P\right)=m_s \cdot g \cdot \left(z_A - z_B \right)\)
Application numérique :
\(W_{AB}\left(\vec P\right)=93 \times 9{,}8 \times (3777 - 1035)\)
\(W_{AB}\left(\vec P\right)\simeq 2{,}50 \times 10^6\ \mathrm J\)
\(W_{AB}\left(\vec P\right)>0\), donc il s'agit d'un travail moteur.