Définition⚓
Définition : Travail d'une force
Le travail d'une force correspond à l’énergie transférée à un système lors d'un déplacement qui induit le déplacement du point d'application de la force. Il s'exprime en joule (J).
Ci-contre, l'illustration d'une situation où la force de traction \({\vec F}_\text{Traction}\), dirigée dans le sens du mouvement, communique de l'énergie au système constitué par le wagon.
Si le point d'application de la force se déplace d'un point A à un point B au cours du mouvement, son travail est noté :

Si \(W_{AB}\left(\vec F \right)>0\), la force \(\vec F\) apporte de l'énergie au système, le travail est moteur.
Si \(W_{AB}\left(\vec F \right)<0\), la force \(\vec F\) fait perdre de l'énergie au système, le travail est résistant.
Expression du travail d'une force⚓
Situation générale
On considère une force \(\vec f\) dont le point d'application se déplace de A en B en suivant la trajectoire réelle représentée en noir sur la figure ci-contre.
On a défini le vecteur déplacement \(\overrightarrow {AB}\).
Plusieurs cas de figure peuvent se présenter selon que la force \(\vec f\) est constante ou non, ou selon sa nature.
Méthode : Cas d'une force constante
Si la force \(\vec f\) est constante (en norme, en direction et en sens) le long du déplacement, alors le travail s'exprime comme le produit scalaire du vecteur force \(\vec f\) et du vecteur déplacement \(\overrightarrow {AB}\).
Complément : Point maths - Produit scalaire de deux vecteurs
Considérons deux vecteurs quelconques \(\vec u\) et \(\vec v\) tels que :
\(\vec u = \begin{pmatrix}u_x \\ u_y\end{pmatrix}\) et \(\vec v = \begin{pmatrix}v_x \\ v_y\end{pmatrix}\) dans un repère orthonormé \(\left(O{,} \vec i{,}\vec j \right)\) ;
\(\widehat{\left(\vec u{,}\vec v \right)} = \alpha\).
Le produit scalaire de \(\vec u\) par \(\vec v\) se note \(\vec u \cdot \vec v\), son résultat est un scalaire (une valeur numérique).
Il peut se calculer de deux manières :
\(\vec u \cdot \vec v=\| \vec u \| \times \|\vec v \| \times \cos \alpha\) ;
\(\vec u \cdot \vec v=u_x \times v_x + u_y \times v_y\), dans le repère orthonormé \(\left(O{,} \vec i{,}\vec j \right)\).
Définition : Force conservative / non conservative
Une force dont le travail ne dépend pas du trajet réellement suivi par le système est dite conservative.
Dans le cas contraire, la force est non conservative.
Méthode : Cas particulier du poids
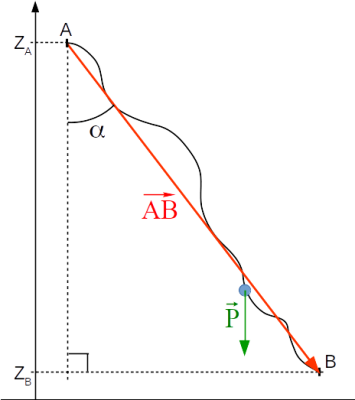
On s'intéresse au travail du poids \(\vec P\) d'un objet qui se déplace selon la trajectoire AB matérialisée en noir.
Le poids étant constant sur tout le trajet, on a :
\(W_{AB}\left(\vec P \right)=\vec P \cdot \overrightarrow{AB}\)
soit \(W_{AB}\left(\vec P \right)=P \cdot AB \cdot \cos\alpha\), avec \(\alpha=\widehat{\left(\vec P{,}\overrightarrow{AB}\right)}\)
Dans le triangle rectangle matérialisé sur la figure ci-contre, \(AB \cdot \cos \alpha = z_A - z_B\).
Donc :
On en conclut que :
Le travail du poids \(\vec P\) lors d'un déplacement ne dépend que des altitudes des points de départ et d'arrivée.
Le travail du poids est donc indépendant du trajet réellement suivi : le poids est une force conservative.
Complément : Pour aller plus loin - Si la force n'est pas constante lors du déplacement (hors programme)
Les calculs précédents s'appliquent à une force constante lors de l'ensemble du déplacement.
Comment calculer le travail de la force si celle-ci varie ?
La trajectoire AB est divisée en déplacement élémentaires infinitésimaux \(\overrightarrow {dl}\) tels qu'on peut considérer la force \(\vec f\) constante sur ce petit déplacement.
On définit donc un travail élémentaire correspondant à ce déplacement infinitésimal :
\(\delta W = \vec f \cdot \overrightarrow {dl}\)
Le travail total pour aller de A en B est alors la somme de tous les travaux élémentaires. La notation est vue dans le programme de mathématiques de la classe de terminale :
\(W_{AB} \left(\vec f \right)=\displaystyle \int_A ^B\vec f \cdot \overrightarrow{dl}\).