Vecteur variation de vitesse
Si un objet est en mouvement rectiligne uniforme, le vecteur vitesse de son centre d'inertie est constant : \(\vec v = \vec{cst}\). Il ne varie ni en norme, ni en direction, ni en sens.
Dans ce cas : \(\Delta \vec v = \vec 0\)
Une fois un objet en mouvement rectiligne uniforme, il n'est pas possible de connaître l'origine de la force qui a initialement provoqué ce mouvement.
La vitesse du centre d'inertie d'un objet est modifiée (modification de sa valeur ou variation de la direction du vecteur) s'il est soumis à une ou plusieurs forces extérieures qui ne se compensent pas, donc telles que \(\sum {\vec F}_{ext} \ne \vec 0\) (lire « Somme des forces extérieures différente du vecteur nul »
).
Dans ce cas \(\Delta \vec v \ne \vec 0\).
Relation entre vecteur variation de vitesse et forces extérieures
Les activités traitées précédemment on permis de montrer que le vecteur variation de vitesse est colinéaire et de même sens que la somme des forces extérieures appliquées à l'objet.
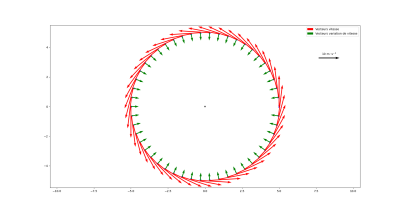
Exemple : Cas d'un mouvement circulaire uniforme
Dans un mouvement circulaire uniforme, le centre d'inertie de l'objet décrit une trajectoire circulaire à vitesse constante.
Le vecteur variation de vitesse pointe vers le centre de la trajectoire, comme on le constate sur la modélisation ci-contre.
Définition : Approche de la deuxième loi de Newton - Rôle de la masse
La deuxième loi de Newton, vue en détails en classe de terminale, relie les variations de la vitesse instantanée par rapport au temps à la somme des forces extérieures appliquées à l'objet. Elle s'applique dans un référentiel galiléen.
Elle fait intervenir la masse dans la relation de colinéarité entre le vecteur variation de vitesse et la résultante des forces extérieures appliquées. Plus la masse d'un corps est grande, plus son inertie, c'est-à-dire sa tendance à maintenir sa vitesse constante, est grande.
Plus la masse d'un corps est importante, plus la résultante des forces à fournir pour modifier sa vitesse est importante.
Cela conduit à la relation approchée de la deuxième loi de Newton ci-dessous :
\(m\) est en kg ;
\(\Delta \vec v\) est en \(\mathbf {m \cdot s^{-1}}\) ;
\(\Delta t\) est en s ;
\(\sum{\vec F}_{ext}\) est en N.
Complément : Un pas vers la terminale
L'approximation de la deuxième loi de Newton est d'autant plus valide que l'intervalle de temps \(\Delta t\) est faible. Elle devient exacte quand cet intervalle tend vers zéro. Si \(\Delta t\) tend vers zéro, \(\dfrac{\Delta \vec v}{\Delta t}\) tend vers la dérivée du vecteur vitesse par rapport au temps, qu'on note en physique \(\dfrac{d \vec v}{dt}\).
Par définition, \(\dfrac{d\vec v}{dt}\) est ce qu'on appelle l'accélération \(\vec a\) de l'objet. La deuxième loi de Newton s'exprime alors dans un référentiel galiléen par la relation :
Cas particulier d'une chute libre
Question⚓
En physique, une chute libre correspond au mouvement d'un objet soumis uniquement à son poids \(\vec P\). Ce n'est donc pas le même sens qu'en parachutisme où la chute libre correspond à la phase du mouvement avant l'ouverture du parachute.
Sur Terre, considérer un objet en chute libre revient à négliger les forces de frottement de l'air.
Ci-contre, la première expérience de chute libre rigoureuse réalisée par David Scott en 1971 lors d'une mission Apollo.
Il lâche simultanément une plume de 30 grammes et un marteau pesant 1,32 kg. En l'absence d'atmosphère, ces deux objets sont en chute libre, soumis à leur poids "lunaire" :
\({\vec P}_{\text {Plume}}=m_{\text {Plume}} \cdot {\vec g}_L\)
\({\vec P}_{\text {Marteau}}=m_{\text {Marteau}} \cdot {\vec g}_L\)
Questions :
Que constate-t-on quant à la chute de ces deux objets sur la Lune ?
Justifier ces observations en démontrant que la variation du vecteur vitesse par rapport au temps \(\dfrac{\Delta \vec v}{\Delta t}\) est indépendante de la masse.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Solution⚓
Pour un corps en chute libre, le bilan des forces se limite à son poids \(\vec P = m \cdot \vec g\)
L'approximation de la deuxième loi de Newton \(m \cdot \dfrac{\Delta \vec v}{\Delta t}=\sum{\vec F}_{ext}\) devient donc :
\(m \cdot \dfrac{\Delta \vec v}{\Delta t}=m \cdot \vec g\)
En simplifiant par la masse m, on a donc :
\(\dfrac{\Delta \vec v}{\Delta t}=\vec g\)
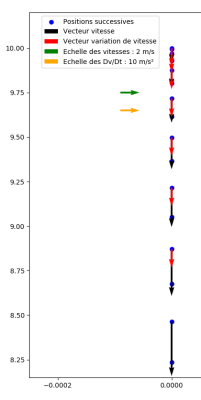
Dans une chute libre, la variation du vecteur vitesse par rapport au temps est égale au champ de pesanteur et est indépendante de la masse de l'objet.
La plume et le marteau ont donc le même mouvement puisque la masse n'intervient pas.
Ci-contre, les représentations des vecteurs vitesse et variation de vitesse par rapport au temps dans le cas d'une chute libre. La vitesse augmente au cours de la chute et la variation du vecteur vitesse est constante.
Complément : Programmes en Python permettant de modéliser les différents mouvement étudiés
Mouvement rectiligne uniforme : RectiligneUniforme.py
Mouvement circulaire uniforme : MouvementCirculaireUniforme_DeltaV.py