Fiche d'activité
Méthode : Étalonnage du dispositif
Le dispositif est étalonné à l'aide du spectre du mercure dont on connaît les longueurs d'ondes des raies principales avec une précision satisfaisante. Lors de la séance de travaux pratiques la raie verte proche de 500 nm n'était pas observable.
Violet | Indigo | Vert | Jaune/Orange |
|---|---|---|---|
\(404{,}7\ nm\) | \(435{,}8\ nm\) | \(546{,}1\ nm\) | \(577{,}5\ nm\) |
Sur l'écran, le spectre est symétrique par rapport à l'image de la fente source. On mesure la distance \(d\) séparant chaque raie de l'image de la fente source avec la plus grande précision possible.
Complément : Incertitude sur la mesure de la distance d
On mesure la distance d avec un réglet dont la précision est \(p=1\ mm=0{,}1\ cm\).
L'incertitude correspond à une double mesure : origine et position de la raie. Dans ce cas de figure on peut montrer que l'incertitude type \(u(d)\) sur la mesure de d se calcule par la relation : \(u(d)=\dfrac{p}{\sqrt 6}\).
Cette incertitude type est la même pour toutes les mesures de d et vaut : \(u(d)\simeq 0{,}041\ cm\).
Mesures expérimentales - Exemple de résultat
\(\lambda\ (nm)\) | \(404{,}7\ nm\) | \(435{,}8\ nm\) | \(546{,}1\ nm\) | \(577{,}5\ nm\) |
|---|---|---|---|---|
\(d\ (cm)\) | 8,1 | 8,8 | 11,4 | 12,0 |
\(u(d)\ (cm)\) | 0,04 | 0,04 | 0,04 | 0,04 |
On obtient la droite d'étalonnage ci-dessous :
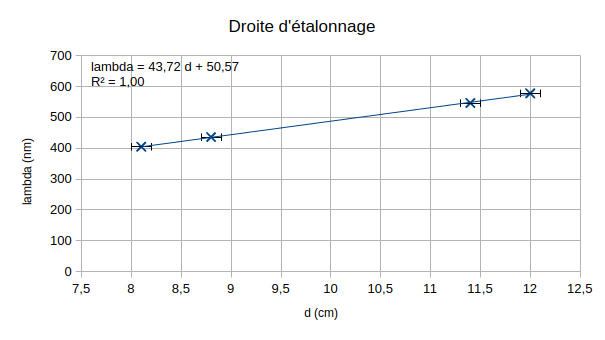
Les barres d'incertitudes sont de faible amplitude et permettent de valider le modèle. Dans la suite on négligera les incertitudes sur le coefficient directeur et l'ordonnée à l'origine de la droite.
On a obtenu la relation mathématique suivante : \(\lambda = a \times d + b\).
Avec :
\(a=43{,}72\ \mathrm{nm \cdot cm^{-1}}\)
\(b=50{,}57\ \mathrm {nm}\)
Détermination de la longueur d'onde de la raie jaune du sodium
Question⚓
Avec le dispositif étalonné précédent, on remplace la lampe à vapeurs de mercure par une lampe à vapeurs de sodium.
On obtient le spectre ci-dessous.
On mesure la distance séparant la raie jaune de l'image de la fente source, sans modifier la configuration du dispositif étalonné : \(d_{Na}=12{,}2\ \mathrm{cm}\).
Déterminer la longueur d'onde de cette raie.
Solution⚓
La relation établie lors de l'étalonnage permet de calculer la longueur d'onde quand on a mesuré la distance qui sépare la raie de l'image de la fente centrale.
\(\lambda_{Na}=\dfrac{d_{Na}-b}{a}\).
Soit numériquement :
\(\lambda_{Na}=\dfrac{11{,}70+0{,}4190}{2{,}0633 \times 10^{-2}} \simeq 587{,}36\ \mathrm{nm}\).
Propagation de l'incertitude sur la valeur de la longueur d'onde
Question⚓
La longueur d'onde est calculée à partir de la mesure de la distance d, à laquelle est associée une incertitude type \(u(d)\). Cette incertitude se propage sur la longueur d'onde calculée.
Avec une hypothèse très simplificatrice, on considère que l'incertitude type sur la longueur d'onde \(u(\lambda)\) découle de \(u(d)\) par la relation \(u(\lambda)=\dfrac{u(d)}{a}\), où a est le coefficient directeur de la modélisation affine calculée précédemment.
Déterminer la valeur de l'incertitude type sur la longueur d'onde \(\lambda_{Na}\).
Écrire la valeur de la longueur d'onde calculée précédemment avec un nombre de chiffres significatifs cohérent avec la précision de l'incertitude type.
Solution⚓
Avec les valeurs calculées précédemment, on a :
\(u(\lambda)=\dfrac{0{,}041}{2{,}0633\times 10^{-2}}\simeq 2{,}0\ \mathrm{nm}\)
En exprimant l'incertitude type sur la longueur d'onde avec deux chiffres significatifs, le chiffre le plus précis correspond au dixième de nanomètre, donc on exprimera le résultat final assorti de son incertitude type sous la forme :
\(\lambda_{Na} = \left(587{,}4\pm 2{,}0 \right)\mathrm {nm}\)
Un pas vers la terminale - Compatibilité de la mesure expérimentale avec la valeur de référence
Question⚓
La longueur d'onde de la raie jaune du sodium, en réalité un doublet dont les longueurs d'onde sont rappelées dans la fiche, vaut \(\lambda^{ref}_{Na}\simeq 589{,}3\ \mathrm{nm}\).
On rappelle le test permettant d'estimer la compatibilité entre une mesure expérimentale et une valeur de référence :
si \(\dfrac{\left|{\lambda_{Na}^{expe}-\lambda_{Na}^{ref}}\right|}{u(\lambda)}<2\), il y a une bonne compatibilité entre la valeur expérimentale et la valeur de référence ;
si \(\dfrac{\left|{\lambda_{Na}^{expe}-\lambda_{Na}^{ref}}\right|}{u(\lambda)}>3\), il y a incompatibilité entre la valeur expérimentale et la valeur de référence.
Déterminer si la compatibilité du résultat pris en exemple dans cette activité est satisfaisante.
Solution⚓
On rappelle le résultat de la mesure dans l'exemple pris pour ce document :
\(\lambda_{Na}^{expe}=587{,}4\ \mathrm{nm}\) ;
\(u(\lambda)=2{,}0\ \mathrm{nm}\).
\(\dfrac{\left|{\lambda_{Na}^{expe}-\lambda_{Na}^{ref}}\right|}{u(\lambda)}=\dfrac{\left|587{,}4-589{,}3 \right|}{2{,}0}\simeq0{,}95\)
Cette valeur est inférieure à 2, donc d'après le critère défini dans la question, la compatibilité entre la valeur expérimentale et la valeur théorique est bonne.
Détermination de la transition énergétique à l'origine de la raie jaune du sodium
Question⚓
On donne ci-contre quelques niveaux d'énergie de l'atome de sodium.
Identifiez la transition énergétique à l'origine de la raie jaune observée et dont la longueur d'onde a été calculée à la question précédente.
Solution⚓
Le photon émis à la longueur d'onde \(\lambda_{Na}=587{,}4 \pm2{,}0\ \mathrm{nm}\) possède une énergie strictement égale à un écart d'énergie entre deux niveaux de l'atome.
La réponse s'effectue en deux temps :
Calcul de l'énergie du photon émis.
Identification de deux niveaux d'énergie séparés de cette valeur.
On calcule l'énergie du photon à l'aide de la relation de Planck-Einstein :
\(E_{photon}=h \times \dfrac{c}{\lambda_{Na}}\)
Application numérique :
\(E_{photon}=6{,}63 \times 10^{-34}\times \dfrac{3{,}00\times 10^8}{587{,}4\times 10^{-9}}\simeq 3{,}39\times 10^{-19}\ \mathrm J\)
Soit en eV :
\(E_{photon}=\dfrac{3{,}39\times 10^{-19}}{1{,}602\times 10^{-19}}\simeq 2{,}12\ \mathrm{eV}\)
L'énergie du photon émis correspond exactement (à l'incertitude près) à l'écart énergétique \(\Delta E\) entre les deux niveaux impliqués.
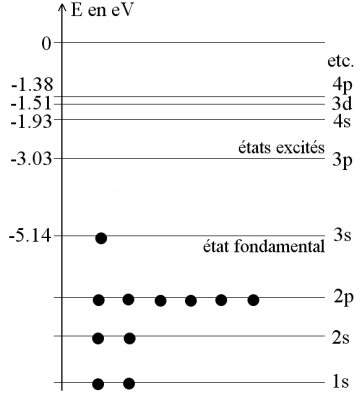
Sur le diagramme des niveaux d'énergie du sodium, on constate que \(\Delta E=E_{3p}-E_{3s}=2{,}11\ \mathrm{eV}\). Aucun autre écart énergétique ne conduit à une valeur correspondant à l'énergie du photon émis.
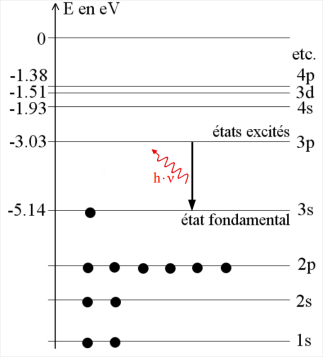
La raie jaune du sodium est donc émise par des atomes de sodium passant de l'état excité 3p à l'état fondamental 3s.
Cette transition énergétique peut se schématiser comme sur la figure ci-contre.
Calcul complémentaire - prise en compte de l'incertitude sur l'énergie du photon
L'incertitude sur la longueur d'onde se propage à l'énergie du photon. Il peut être nécessaire de déterminer l'incertitude élargie sur l'énergie du photon pour s'assurer de l'unicité du \(\Delta E\) associé. Si cette incertitude est trop importante, plusieurs transitions énergétiques peuvent correspondre et on ne peut pas trancher précisément.
On peut montrer que l'incertitude élargie sur l'énergie est donnée par la relation :
\(u(E)=\dfrac{h \cdot c}{\lambda^2}\cdot{u(\lambda)}\)
Soit numériquement :
\(u(E)=\dfrac{6{,}63\times 10^{-34}\times 3\times10^8}{\left(587{,}4\times 10^{-9}\right)^2}\times 2{,}0\times 10^{-9}\simeq1{,}2\times 10^{-21}\ \mathrm J\), soit en eV \(u(E)=7{,}2\times 10^{-3}\ \mathrm{eV}\)
L'incertitude type sur la valeur de l'énergie du photon est faible, donc il n'y a pas d’ambiguïté sur la transition énergétique concernée. Seule la transition 3p → 3s est possible.