Raies les plus intenses du spectre de l'atome de mercure
Le spectre d'émission ci-dessous a été obtenu avec une lampe à vapeur de d'atomes de mercure.
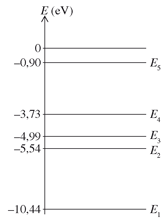
Niveaux d'énergie de l'atome de mercure
La figure ci-contre montre le diagramme énergétique de l'atome de mercure qui répertorie les énergies de quelques niveaux.
Chaque énergie est associée à une configuration électronique particulière.
Identifier la raie correspondant à une transition énergétique donnée
Question⚓
Identifier sur le spectre d'émission de l'atome de mercure la raie correspondant à la transition \(E_5 \rightarrow E_4\).
Solution⚓
On cherche à identifier la longueur d'onde du photon émis lorsqu'un atome de mercure passe du niveau d'énergie E5=-0,90 eV et E4=-3,73 eV.
On commence par calculer l'énergie correspondant à cette transition énergétique :
\(\Delta E=E_5-E_4=-0{,}90-(-3{,}73)=2{,}83\ \mathrm{eV}\)
Le photon émis possède donc une énergie \(E_{photon}=2{,}83\ \mathrm{eV}\).
La détermination de la fréquence et de la longueur d'onde se fait en exploitant la relation de Planck-Einstein après avoir pris soin d'exprimer l'énergie en joules.
\(E_{photon}=2{,}83 \times 1{,}602 \times 10^{-19} \simeq 4{,}53 \times 10^{-19}\ \mathrm J\).
La relation de Planck-Einstein permet de calculer la fréquence du photon :
\(E_{photon}=h\times \nu\), donc \(\nu=\dfrac{E_{photon}}{h}\).
Application numérique : \(\nu=\dfrac{4{,}53 \times 10^{-19}}{6{,}63 \times 10^{-34}} \simeq 6{,}83\times 10^{14}\ \mathrm{Hz}\).
On obtient la longueur d'onde par la relation \(\lambda=\dfrac{c}{\nu}\), soit numériquement : \(\lambda=\dfrac{3{,}00\times 10^8}{6{,}83\times 10^{14}}\simeq 4{,}39\times 10^{-7}\ \mathrm m\simeq 439\ \mathrm{nm}\).
Le photon correspondant à la transition du niveau 5 vers le niveau 4 a donc une longueur d'onde de 439 nm. Cette raie est bien présente sur le spectre de l'atome : c'est la deuxième raie bleue en partant de la gauche du spectre.
On a ainsi établi la correspondance entre une transition énergétique et une raie visible sur le spectre.